Information-theoretic security

A cryptosystem is information-theoretically secure if its security derives purely from information theory. That is, it is secure even when the adversary has unlimited computing power. The adversary simply does not have enough information to break the security. An algorithm or encryption protocol that has information-theoretic security does not depend for its effectiveness on unproven assumptions about computational hardness and such an algorithm is not vulnerable to future developments in quantum computing. An example of an information-theoretically secure cryptosystem is the one-time pad.

An interesting special case is perfect security: an encryption algorithm is perfectly secure if a ciphertext produced using it provides no information about the plaintext without knowledge of the key. If E is a perfectly secure encryption function, for any fixed message m there must exist for each ciphertext c at least one key such that 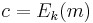. There is also a weaker notion of security defined by A. Wyner and followed by many people in the area of information theory recently.^[1]

It is common for a cryptosystem to leak some information but nevertheless maintain its security properties even against an adversary that has unlimited computational resources. Such a cryptosystem would have information theoretic but not perfect security. The exact definition of security would depend on the cryptosystem in question.

There are a variety of cryptographic tasks for which information-theoretic security is a meaningful and useful requirement. A few of these are:

1. Secret sharing schemes such as Shamir's are information-theoretically secure (and also perfectly secure) in that less than the requisite number of shares of the secret provide no information about the secret.
2. More generally, secure multiparty computation protocols often, but not always have information theoretic security.
3. Private information retrieval with multiple databases can be achieved with information-theoretic privacy for the user's query.
4. Reductions between cryptographic primitives or tasks can often be achieved information-theoretically. Such reductions are important from a theoretical perspective, because they establish that primitive 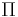can be realized if primitive 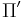can be realized.
5. Symmetric encryption can be constructed under an information-theoretic notion of security called entropic security, which assumes that the adversary knows almost nothing about the message being sent. The goal here is to hide all functions of the plaintext rather than all information about it.
6. Quantum cryptography is largely part of information-theoretic cryptography.

Unconditional security

Information-theoretic security is often used interchangeably with unconditional security. However the latter term can also refer to systems that don't rely on unproven computational hardness assumptions. Today these systems are essentially the same as those that are information-theoretically secure. However it does not always have to be that way. One day RSA might be proved secure, thus becoming unconditionally secure, but it will never be information-theoretically secure.

See also

• Leftover hash-lemma (Privacy amplification)
• Semantic security

References

Russell, Alexander; Wang, Hong (2002). Knudsen, Lars. ed. "How to fool an unbounded adversary with a short key" (PDF). Advances in Cryptology — EUROCRYPT 2002. Lecture Notes in Computer Science (Springer Berlin / Heidelberg) 2332: 133–148. doi:http://dx.doi.org/10.1007/3-540-46035-7_9. http://www.engr.uconn.edu/~acr/Papers/encryption-euro-final.pdf. Retrieved 11 August 2010.